Détermination de la distance focale d'un instrument
La manip consiste à faire traverser le capteur de la webcam à une étoile de déclinaison connue, la webcam étant placée au foyer de l'instrument.
Aligner la plus grande largeur du capteur de la webcam avec l'ascension droite,
en déplaçant l'étoile dans le champ du capteur vérifier qu'elle se déplace bien parallèlement au bord du champ.
Arrêter le suivi sidéral de la monture
Sortir l'étoile du champ (du bon côté) de manière à ce qu'elle y entre à nouveau dans quelques secondes
Lancer une capture vidéo
L'étoile traverse alors le champ du capteur, de gauche à droite dans mon cas :
Capturer plusieurs traversées en vue d'avoir une meilleure précision
Repérer les instants d'entrée et de sortie avec l'indicateur de position de Virtualdub (par exemple) :

afin de déduire le temps de traversée.
Résultats pour la lunette 70/700 et le téléscope 114/900 :
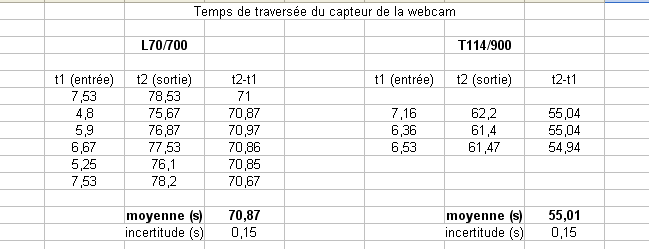
Connaissant la taille réelle du capteur dans sa plus grande largeur (640 pixels de 5,6µm),
la période de rotation sidérale de la Terre (23h 56min 4s)
et la déclinaison de l'étoile (ici Regulus d = 11°58'),
on remonte alors à la focale de l'instrument (en mm) :
f = (640 / 2) x 5,6 x 10^-3 / tan (360 x t x cos d / (86164 x 2))
(sans aucune approximation du fait de l'angle faible)
Avec approximation angle faible :
f = 640 x 5,6 x 10^-3 / (2 x pi x t x cos d / 86164 )
Formule simplifiée pour capteur 640 pixels de 5,6 µm :
f = 49149 / ( t x cos d )
Il vient alors :
f = 709 +- 2 mm pour la lunette
f = 913 +- 3 mm pour le téléscope
Remarques :
Quid de la précision pour la taille du pixel de 5,6 µm ??? Un chiffre significatif supplémentaire serait le bienvenu.
Un règle de trois sur l'image d'un objet de dimension connu comme le diamètre lunaire permet de s'affranchir de la taille du pixel.